BlackGhost

Transformation变换(1)

1.基础变换

引入齐次坐标，对于二维平面：
点 (x, y) ，其齐次坐标为：(x, y ,1)
向量(x, y)，其齐次坐标为：(x, y, 0)
可以保证加减性质不变：

想一想：点 + 点表示的是上面：

表示的是两个点连线的中点、

1.1 缩放

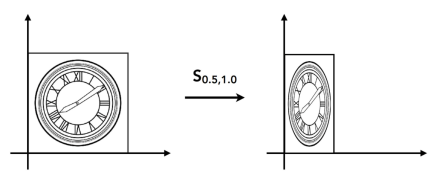
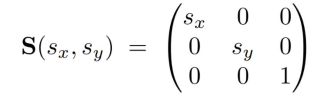
1.2旋转

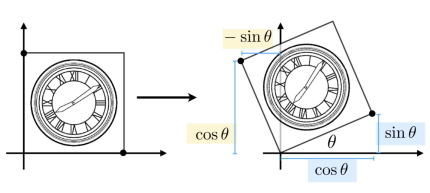
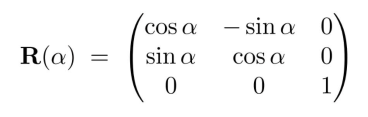
1.3平移

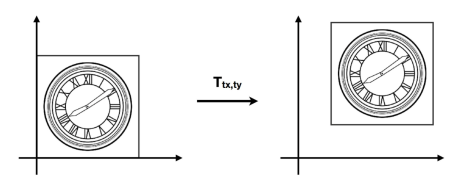
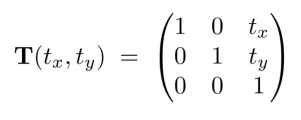
1.4仿射变换

仿射变换 = 线性变换 + 平移变换

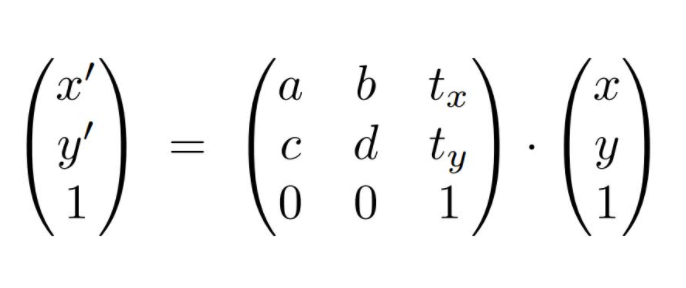
1.5复合变换

多个简单的变换矩阵可以组合成一个矩阵（相乘即可，注意顺序）
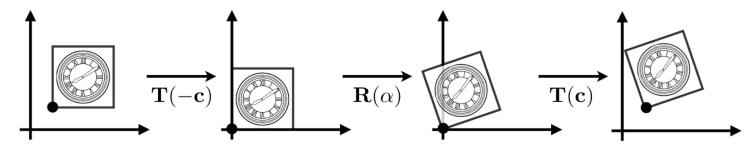
比如要将某个点绕着一个非原点的点（a, b）旋转a度，可以进行如下操作：
思路：

1. 我们先把点(a,b)看成原点，这就需要先做平移变换，将点平移(-a,-b)

2. 然后绕着原点旋转a度

3. 然后把点平移(a,b)

   

1.6逆变换

观察旋转矩阵,逆时针旋转 a 角度
$$
A =
\begin{bmatrix}
\cos(\alpha) & -\sin(\alpha) \
\sin(\alpha) & \cos(\alpha) \
\end{bmatrix}
$$
若要旋转 -a 角度，则其变换矩阵为：
$$
B =
\begin{bmatrix}
\cos(\alpha) & \sin(\alpha) \
-\sin(\alpha) & \cos(\alpha) \
\end{bmatrix}
$$
显然可以看出:
$$
A * B = E
$$
转置矩阵与逆矩阵相等的矩阵称为正交矩阵。 且所有的旋转矩阵都是正交矩阵

2.3D变换

3维空间同样适用二维的齐次坐标规则
3维的仿射变换：

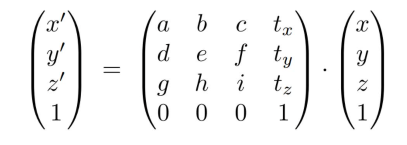
2.1缩放

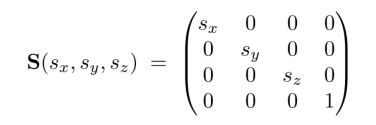
2.2平移

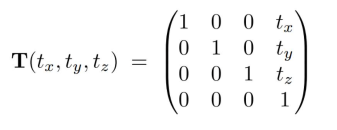
2.3旋转

2.3.1绕某一个轴旋转

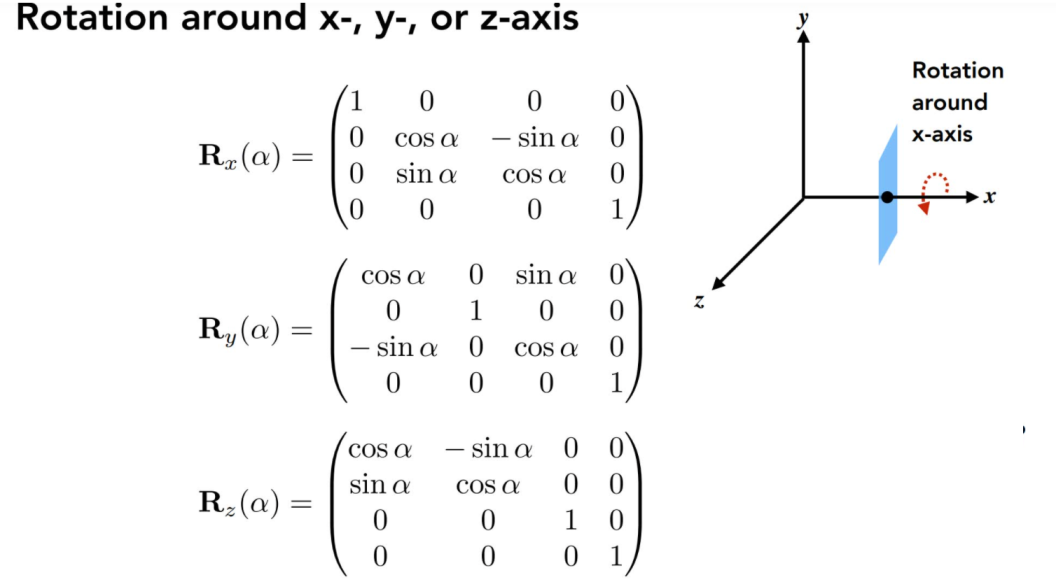
• 注意：这里的绕y轴旋转公式与x和z轴有所不同。
• xyz坐标系, x叉乘y得z, y叉乘z得x，y等于z叉乘x。xyz轴的关系：z-xy, x-yz, y-zx

2.3.2任意旋转

任意角度的旋转都可以转换成绕x、y、z轴的旋转的组合
Rodrigues 旋转公式：

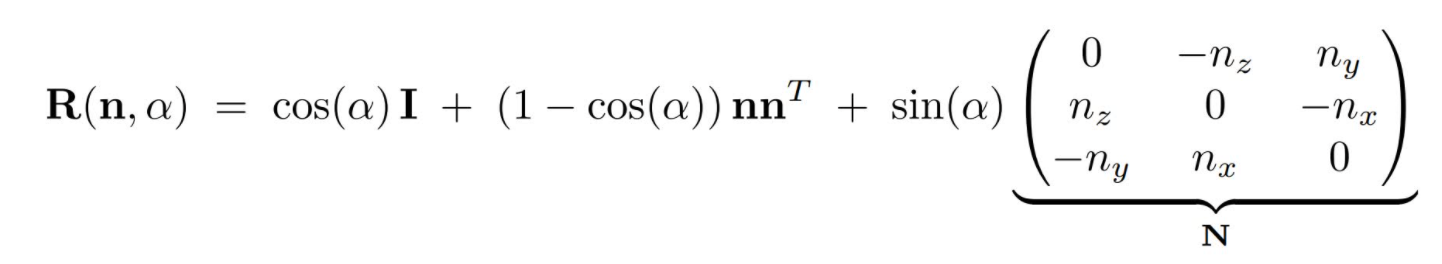
其是3阶单位矩阵，矩阵 其实就是向量的叉积矩阵（被该矩阵作用得到的结果 等同于 与n向量叉积的结果）